Knuth’s “Why Pi” Talk at Stanford: Part 1

A few weeks ago I had another opportunity to meet a giant in my field: Donald Knuth was giving his annual Christmas Tree lecture at Stanford, where I happened to be near at the time. The most exciting part was probably right at the very beginning, when Knuth announced that, for the first (“and probably only”) time, he had finished two books on that same day: The Art of Computer Programming: Volume 4A, and Selected Papers on Fun and Games, with the pre-order links on Amazon going up the same day.

The topic of this year’s lecture was, according to the site:

Mathematicians have known for almost 300 years that the value of n! (the product of the first n positive integers) is approximately equal to, whereis the ratio of the circumference of a circle to its diameter. That’s “Stirling’s approximation.” But it hasn’t been clear why there is any connection whatever between circles and factorials; the appearance ofhas seemed to be purely coincidental, one of the amazing accidents of nature. Recently however Johan Wästlund has found a nice explanation of this phenomenon, and the reason turns out to be connected with the theory of trees.

I found the lecture originally hard to follow; although Knuth is now 74 years old and physically growing quite frail, his mind was still evidently much sharper than the audience’s; he was completely prepared for every question regarding extensions and corner cases of the material he was presenting. I considered the notes I took to be somewhat useless since I had spent so much time just trying to follow his reasoning. However, when the video became available, I had no excuse left, so I went through it again armed with a pen and the pause button, and I now have a set of notes somewhat worthy of posting here for anyone who missed it. Any errors or inconsistencies are almost definitely my fault and not his.

The notes themselves are after the jump.

The Knight Metric

Here’s a problem I’ve been thinking about. I’m curious if anybody has any ideas about it; I have reasons to believe it might be very hard (in the theoretical sense) but I haven’t given it much time yet.

Consider a (possibly infinite) two-dimensional integer grid , with some finite subset of its cells colored black. We consider two cellsto be connected if ; that is, if the cells are a knight’s move apart. Write a function that computes the least number of additional cells that would need to be colored black in order to ensure that there exists a connected path between any two black cells.

The trickiness comes from the fact that adding a black square can either increase or decrease the total number (it’s not hard to come up with examples of either possibility), so the problem resists simplification. I have no idea if this can be computed in polynomial time or space. I thought of it in the context of geometric constructions, for which computability results are notoriously difficult, but it smells like this can be solved in purely graph-theoretic terms. There is actually a closed formula for the “knight’s distance” between two points, though it is a bit complicated:

where and. If we take each pair of given black squares, calculate their shortest distance, we can use that as an admissible heuristic to an A^* search to find the shortest paths in polynomial time. Easy.

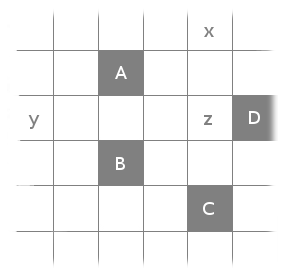
Except that it doesn’t work. It’s minimizing the wrong thing: distance, instead of the minimum number of squares. Consider the following configuration:

Figure A

It’s easy to see that there’s (two) ways to solve this problem by adding just a single square (either x or y). Therefore, the answer to our problem is 1. However, the above approach would instead notice that it could make all the distances be less than or equal to 2 by adding x and y and z, while adding just x would makeand just y would make.

Thus the problem has some non-local properties that I don’t really know how to translate into graph-theoretic terms, unless I just consider all paths within a certain ball whose size is linear in the diameter of the graph, but that would be exponential.

If anyone has any clever ideas, I’d be interested in hearing about it.

Scheme Discovery

This little program was inspired partly by some Tcl code by Richard Suchenwirth, but mostly by my in-progress reading of Gödel, Escher, Bach (which carries my highest recommendation, by the way).

The basic idea is like this: create a simple little bytecode language where every possible string from the alphabet is well-formed. Write an interpreter for this “language”. Then, find some way to enumerate all the possible strings in the language (in this case, using something quite similar to Gödel numbering). Lastly, using this numbering, iterate through all possible strings looking for a program that will match a given set of input-output parameters you provide. Put all these together and what do you get? A program that is able to generate its own algorithms to solve some simple problems! I implemented this in Scheme.

(define stack (list))
(define cmd (make-hash-table 'equal))
(define cmd-stack-balance (make-hash-table 'equal))

The easiest way to have this bytecode language operate is on a single global stack. The ‘inputs’ will be the initial state of the stack, and the ‘output’ will be the state of the stack when the last character in the bytecode has been executed. We will also keep a hash table containing the operation associated with each character of the alphabet of the bytecode language. Lastly, we have the cmd-stack-balance hash table, which will serve an optimization purpose later on.

(define (push val)
     (set! stack (cons val stack)))
(define (pop)
     (begin (define tmp (first stack)) (set! stack (rest stack)) tmp))
(define (swap) (begin (define tmp1 (pop))
                      (define tmp2 (pop))
                      (push tmp1) (push tmp2)))

Next we implement a lot of the basic stack operations we’ll need in order to build the bytecode language. None of this needs explaining, I trust.

(define alphabet '(+ - * / d q ^ s))
(hash-table-put! cmd '+ (lambda () (push (+ (pop) (pop)))))
(hash-table-put! cmd '- (lambda () (begin (swap) (push (- (pop) (pop))))))
(hash-table-put! cmd '* (lambda () (push (* (pop) (pop)))))
(hash-table-put! cmd '/ (lambda () (begin (swap) (push (/ (pop) (pop))))))
(hash-table-put! cmd 'd (lambda () (push (first stack))))
(hash-table-put! cmd 'q (lambda () (push (sqrt (pop)))))
(hash-table-put! cmd '^ (lambda () (push (expt (pop) (pop)))))
(hash-table-put! cmd 's (lambda () (swap)))

Next we implement the individual commands of our bytecode language. This part is entirely configurable; you can add more commands if you want, as long as you maintain the rule that all strings are well-formed. In my case here, I have the four simple arithmetic rules, (+ – / *) which pop two values off the stack, perform the operation, and push the result. I also have a simple exponentiation command (^), a simple square root command which acts on the popped value from the stack (q), a duplicate command which pops a value from the stack and then pushes it twice, and a swap command which pops two values and pushes them back in the order they were received. This is all I’m going to use for this language, so now it is time to implement the function which execute these bytecode strings.

(define (evaluate-bytecode code in)
  (define (evaluate-bytecode-helper opcodes)
            (cond
               ((empty? opcodes) void)
               ((not (empty? opcodes))
                (with-handlers ((exn:fail? (lambda (x) '(ERROR))))
                  ((hash-table-get cmd (first opcodes)))
                  (evaluate-bytecode-helper (rest opcodes))))))
    (set! stack in)
    (evaluate-bytecode-helper code)
    stack)

As a side note, this was the only time I had to look up any new Scheme syntax beyond what was taught in my CS 136 course, since exception-handling was not covered. Everything else is doable with only that course under your belt. Because of the simple nature of our language, the bytecode interpreter borders on trivial. We simply recurse on each character of the bytecode string, passing the character to the cmd hash table to obtain the corresponding function, we eval it, and once we’ve exhausted the string, we simply return a reference to the global stack. The caveat here is that we may try to pop more values off the stack than are present. In this case we simply catch the exception and return junk. The reason for this behavior will become obvious in a few minutes. This restriction doesn’t really violate our condition that all strings be well-formed; they are still valid bytecode strings, but they do not have any meaning in the current context (this important distinction is one of the key messages of Gödel, Escher, Bach.)

(define (godelize num alpha)
  (local ((define (godelize-helper num word length)
            (cond
              ((<= num 0) (reverse word))
              (else (godelize-helper (quotient (sub1 num) length)
                                     (append word (list (list-ref alpha
                                                          (remainder (sub1 num) length)))) length)))))
    (godelize-helper num (list) (length alpha))))

This function defines the mapping between positive integers and bytecode strings. It’s not hard to see that this mapping is one-to-one and onto (an isomorphism); it’s even easier to see a few important properties, like higher numbers corresponding to longer bytecode strings. Most importantly we now have an effective way of generating an iterable list of words. What we eventually want to do is specify a set of input/output pairs (like '((3) (4) (5) (6)) ) and have our program find bytecode strings that match them (hopefully, in this case, a successor function). The important thing to note is that there is a relationship between the number of elements on the input stack and the number of elements on the output stack; if our desired output has the same number of elements on the stack as the input stack, for instance, we can disqualify any strings composed entirely of +,-,*,/ without even executing them, because these operations always diminish the size of the stack by one. More generally, every command has a predictable effect on the size of the stack. When we generate our set of strings, before we start executing any of them, we can go through the list beforehand and filter out any strings that do not even meet the basic requirement of stack balance. Thus we’ll need another map that keeps track of how each command affects the stack balance, and a function that calculates the overall stack balance of a string based on those numbers:

(hash-table-put! cmd-stack-balance '+ -1)
(hash-table-put! cmd-stack-balance '- -1)
(hash-table-put! cmd-stack-balance '/ -1)
(hash-table-put! cmd-stack-balance '* -1)
(hash-table-put! cmd-stack-balance 'd +1)
(hash-table-put! cmd-stack-balance 'q 0)
(hash-table-put! cmd-stack-balance '^ -1)
(hash-table-put! cmd-stack-balance 's 0)
(define (calc-stack-balance bc)
  (foldr + 0 (map (lambda (x) (hash-table-get cmd-stack-balance x)) bc)))

And now finally we can attack the meat-and-potatoes of our algorithm. We will choose an upper bound of how many strings to generate (based mainly on how long we feel like waiting around for our program to execute), an alphabet (the one we just made), and a set of input/output pairs. Next we will generate our search space by iterating through all the numbers between 1 and our upper bound, “Gödelizing” them all on the way. Then we filter that search space by stack balance in order to significantly cut our workload. Finally, we iterate through our space one by one, checking each string against the desired outputs. If we find something that meets all of our conditions, we happily exit and proclaim our newfound discovery!

(define (generate-search-space alphabet lower upper)
  (map (lambda (x) (godelize x alphabet))
       (build-list (add1 (- upper lower)) (lambda (x) (+ x lower)))))
(define (filter-search-space space sb)
  (filter (lambda (x) (= sb (calc-stack-balance x))) space))
(define (discover params limit alphabet)
  (define sp (filter-search-space (generate-search-space alphabet 1 limit)
                                  (- (length (first (rest params)))
                                     (length (first params)))))
  (define (search-space space)
    ;(display (exact->inexact (* 100 (/ (length space) (length sp)))))
    ;(display #newline)
    (cond ((empty? space) (display "Could not find a suitable algorithm."))
          (else (result-check params space))))
(define (result-check remaining_tests space)
    (cond ((empty? remaining_tests) (display "Found!") (display (first space)))
          (else
           (cond ((equal? (evaluate-bytecode (first space) (first remaining_tests))
                          (second remaining_tests))
                  (result-check (rest (rest remaining_tests)) space))
                 (else (search-space (rest space)))))))
(search-space sp))

As a side note, you can see the cute use of mutual recursion in the discovery helper methods there; search-space passes control over to result-check, who, in the likely event of a non-match, passes back control to search-space, but removing itself from the list.

Finally we are ready for testing!

> (discover '((3) (4) (5) (6) (7) (8)) 50000 alphabet)
Found! (d d / +)

Hmm… this looks like a strange way to implement as something as simple as a successor function. Let’s trace one of the cases.

Stack: (3)
Stack: (3 3)     (d = duplicate)
Stack: (3 3 3)   (d = duplicate)
Stack: (1 3)     (/ = divide, and 3/3=1)
Stack: (4)       (+ = add, and 3+1=4)

Indeed, we do arrive at four, and it is not hard to see that this will work for all positive integers. We can do a few other simple ones:

> (discover '((8) (4)) 50000 alphabet)
Found!(d + q)
> (discover '((1 1 5) (7) (2 3 8 ) (13) (1 10 6) (17)) 50000 alphabet)
Found!(+ +)
> (discover '((0) (1) (1) (2)) 500000 alphabet)
Found!(d d + ^)

Note that these are all “correct” though they may not be exactly what you were looking for or intending 😉

The problem is, the search space grows exponentially fast, and even relatively simple problems can take hours to find in the interpreter. I suppose using mzc to compile this would be a step in the right direction but I suspect it would still not help much for strings longer than 7 or 8.

But refactoring, optimizing, and redesigning this algorithm for performance is a job for another day 🙂