S3FS

A short while ago, I took a renewed interest in Randy Rizun’s S3FS project (which had mostly been stagnating) and cloned it to GitHub. It’s basically a FUSE module backed by an S3 bucket. It’s often used on EC2 instances to provide a shared persistent store (which means no EBS); nothing too fancy, but it nicely combines several of my technical interests. I began cleaning it up to prepare it for packaging to Debian and Gentoo, which involved moving it to Autotools, when I was contacted by another developer who had simultaneously decided to rehabilitate the project as well. He had taken the extra effort of contacting Randy about getting us commit access to the original project, which was swiftly granted, so now those changes have been rolled in. Dan also fixed up a lot of outstanding issues, and I’ve started refactoring the old code. The renewed activity must have caught users’ attention as well, because we’ve started getting patches, such as this one to cache read-only files. So it looks like there’s bright things in store for S3FS! Some of the things on my road map (and I don’t speak for Dan here) are:

• .debs and .ebuilds for inclusion into (at least) the distributions I’m familiar with, and which are commonly used with EC2.
• Port to MacFUSE.
• GVFS/KIO wrappers for proper integration into Gnome/KDE. I haven’t done much research into this one yet, so I’m not sure how much of an undertaking this will turn out to be.
• Intelligent caching.
• Some rudimentary mapping of ACLs to Unix permissions.
• General code clean-up and refactoring.

So, this post is for people searching on information about S3FS to stumble on and know what’s in store for the project.

The Knight Metric

Here’s a problem I’ve been thinking about. I’m curious if anybody has any ideas about it; I have reasons to believe it might be very hard (in the theoretical sense) but I haven’t given it much time yet.

Consider a (possibly infinite) two-dimensional integer grid , with some finite subset of its cells colored black. We consider two cellsto be connected if ; that is, if the cells are a knight’s move apart. Write a function that computes the least number of additional cells that would need to be colored black in order to ensure that there exists a connected path between any two black cells.

The trickiness comes from the fact that adding a black square can either increase or decrease the total number (it’s not hard to come up with examples of either possibility), so the problem resists simplification. I have no idea if this can be computed in polynomial time or space. I thought of it in the context of geometric constructions, for which computability results are notoriously difficult, but it smells like this can be solved in purely graph-theoretic terms. There is actually a closed formula for the “knight’s distance” between two points, though it is a bit complicated:

where and. If we take each pair of given black squares, calculate their shortest distance, we can use that as an admissible heuristic to an A^* search to find the shortest paths in polynomial time. Easy.

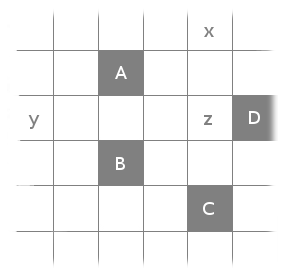
Except that it doesn’t work. It’s minimizing the wrong thing: distance, instead of the minimum number of squares. Consider the following configuration:

Figure A

It’s easy to see that there’s (two) ways to solve this problem by adding just a single square (either x or y). Therefore, the answer to our problem is 1. However, the above approach would instead notice that it could make all the distances be less than or equal to 2 by adding x and y and z, while adding just x would makeand just y would make.

Thus the problem has some non-local properties that I don’t really know how to translate into graph-theoretic terms, unless I just consider all paths within a certain ball whose size is linear in the diameter of the graph, but that would be exponential.

If anyone has any clever ideas, I’d be interested in hearing about it.

Java puzzler: Generic type inference

Here’s an issue I ran into while hacking a type system to work with some very inflexible generated code; I’ve distilled the strangeness into the simplest form I could.

Suppose you have a simple type hierarchy:

public class A { }
public class B extends A { }
public class C extends A { }

Then, it turns out that the following code works just fine:

List<Class<? extends A>> list = ImmutableList.of(B.class, C.class);

Surprisingly, however, the following code fails to compile(!):

List<Class<? extends A>> list = ImmutableList.of(B.class);

with the error

incompatible types
found   : com.google.common.collect.ImmutableList<java.lang.class<B>>
required: java.util.List<java.lang.class<? extends A>>
    List<Class<? extends A>> list = ImmutableList.of(
    ...

 

That’s right; adding the parameter makes this typesafe! (Note that my example uses ImmutableLists from the Google Common Collections, but this is actually happening because of Java’s type inference mechanism, not anything related to that particular class). Of course, it’s easy to work around it, but the interesting thing is what can be learned about Java by understanding the problem here.

I’ll post a “solution” in a few days, in case anyone wants to give it a shot.